This page is under construction.

Table of Contents

  1. What is CP Symmetry?
  2. The Discovery of CP Violation
  3. Why is CP Violation Important?
  4. CP Violation in Hyperon Decays

What is CP Symmetry?

There are three fundamental discrete symmetries in nature: charge conjugation C, which takes a particle and transforms it into an antiparticle; parity inversion P, which reverses the sign of all the coordinates; and time reversal T, which reverses the direction of time. It can be shown using very general arguments, that all theories must be invariant under the product of the three: CPT.

It was long thought that all theories of nature were also invariant under each of C, P, and T separately as well. That is, until 1957 when parity was found not to be a good symmetry of nature. Since CPT had to be invariant, the fall of parity conservation meant that either C, or T, or perhaps both had to be violated as well. It was soon found that C was violated.

Landau noticed, however, that CP seemed to be a good symmetry, and suggested that it, rather than C alone is the correct transformation to go from matter to antimatter. We can see this in the figure below. One of the carriers of the weak force, the W-, is known to decay into an electron and an electron anti-neutrino, where the spin of the electron is in the opposite direction to its momentum (we say it is in an anti-helicity state), and the spin of the anti-neutrino is in the direction of its momentum (we say it is in a helicity state). Under charge conjugation (C), the W- is transformed into a W+, the electron, to a positron, and the anti-neutrino into a neutrino, with the helicities unaffected. But such a decay of the W+ does not occur in nature! We do see it decaying into a positron and an electron neutrino, but not with same helicities as in the W- decay. That is, neutrinos with a positive helicity have never been seen in nature.

However, if we go one step further, and transform the illegal W+ decay using the parity (P) operation, then we find something very interesting. Parity changes the direction of the momentum vectors of the positron and neutrino, but it doesn't affect the spin or angular momentum of each. So it effectively changes the helicity of a particle. We end up with a positron of postive helicy and an electron neutrino of negative helicity. These neutrinos do exist in nature and such a decay of the W+ has indeed been observed. So it appears that parity violation is compensated by a failure of charged conservation and CP is the correct `mirror' that takes us from the world to the anti-world.

The Discovery of CP Violation

For a while it looked like Landau's hypothesis was good and though both C and P were violated maximally in weak interactions, CP was a good symmetry of nature. Then in 1964 Christenson, Cronin, Fitch, and Turlay reported a small, but significant violation of CP in the decay of the K-meson. It was known at the time that there were two neutron kaons, one with CP odd and the other with CP even. To conserve CP, the CP-odd kaon had to decay into three pions and the CP-even kaon had to decay into two pions. Because the phase space to decay into three pions is very small relative to the two-pion phase space, the rate into two pions is much greater, and hence the lifetime of the CP-even kaon is much shorter (by about a factor of 500). Hence the CP-even kaon is called the KS (S for 'short') and the CP-odd kaon is called the KL (L for 'l

Cronin and Fitch's experiment showed that about one KL in 500 decays into two pions, the wrong CP state, rather than three pions. Hence CP is violated. To this day CP violation still has only been seen in the decay of the KL. (To be precise, in four decay modes of the KL.) And it is now known that the CP violation comes about through the mixing of KS and KL -- through the so-called box diagrams shown below -- and not directly in the weak decay of the KL. Hence we call this indirect CP violation. Direct CP violation should be present to some level in most weak decays if our standard model picture of CP violation is correct. To date however, there is no compelling evidence for direct CP violation and no evidence for CP violation outside of the decay of the KL. HyperCP addresses both of these issues.

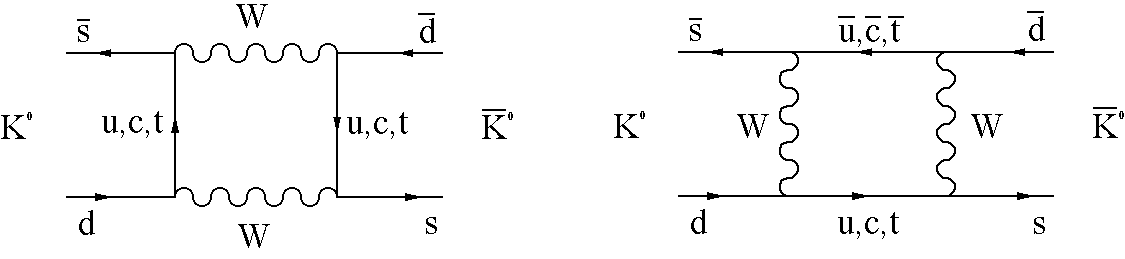
Why is CP Violation Important?

Any fundamental symmetry violation is important and must be understood. So for that reason alone CP violation should be studied. But unlike parity violation, CP violation could have macroscopic consequences on a grand scale. Indeed, it could be the reason we are here at all!

In the Big Bang theory of the Universe, at early times (less than one microsecond) the Universe was a very hot plasma composed of equal amounts of quarks and anti-quarks, leptons and anti-leptons. That is, the net baryon number of the universe (the amount of matter minus the amount of anti-matter) was zero. After about a microsecond baryons and anti-baryons began to be formed as the Universe cooled down. The Universe was dense enough at this time, and until about one millisecond, that the baryons and anti-baryons should have almost all mutually annihilated, producing photons. What should have been left was a very small and equal number of baryons and anti-baryons, the total number divided by the number of photons being about 10-18. What we observe is quite different. There is no compelling evidence for any antimatter in the Universe (expect at accelerators such as Fermilab!) and the ratio of baryons to photons isn't 10-18, but about 10-10. That is, eight orders of magnitude too large! So the Big Bang almost produced an equal amount of matter and antimatter, but not quite: for every 10 billion anti-baryons, 10 billion and one baryons were produced.

What happened to cause this asymmetry between matter and anti-matter in the Universe. We only have one theory that has a chance of explaining the asymmetry, a theory due to Sakharov. There are three ingredients needed to generate such an asymmetry.

  1. A baryon nonconserving interaction.
  2. Violation of both C and CP.
  3. A departure from thermal equilibrium when the baryon number was being violated.
So in theory, the CP violation that we have observed in experiments on Earth could be the reason for this asymmetry between matter and anti-matter, and why we are here. If so, it would be the first link between a macroscopic asymmetry in nature and a fundamental symmetry violation.

CP Violation in Hyperon Decays

What are Hyperons?

Hyperons are baryons, that is, particles composed of three quarks, like the proton and neutron, that have one or more strange quarks. A Lambda hyperon is composed of an up, down and strange quark, and a Xi- hyperon is composed of a down and two strange quarks. They have relatively long lifetimes, and decay via the weak interaction as shown in the figure below.

The Xi- decays almost exclusively into a Lambda and a pi-, whereas the Lambda decays about two-thirds of the time into a proton and a pi-, and about one-third of the time into a neutron and a pio. When the Lambda decays into a proton and pi-, it is experimentally observed that the proton predominantly is found going off in the direction of the spin of the Lambda. That is the decay distribution is not isotropic. Hence, as shown in the figure below, the decay violates parity conservation. The same is true with the decay of the Xi-.