Fermilab
|
Doc. No. : Beams-doc-1148
Old Doc. No. : MI-0209
Version : 4.0
The objectives of this document are to relate Fermilab
to a global coordinate system, to define a mapping projection
and establish all the coordinate systems that will be used at
Fermilab and for the Fermilab Main Injector
(FMI) project, and to describe all the parameters
that are necessary for the several coordinate systems. The main
objective is to define a new assimilated DUSAF coordinate
system for the Fermilab site. This implies that the new system
will have the same origin and coordinate axes definitions as the
DUSAF coordinate system. The Survey Alignment and Geodesy (SAG)
group, has defined a Fermilab Site Coordinate System (FSCS)
for the site and a Local Tunnel Coordinate System (LTCS)
for the FMI project. A Double Stereographic Projection has
been adopted to define both coordinate systems.
Table of Contents
6. Local Geodetic System (LGS)
7. Oblique Mercator Projection System (OMPS)
8. Illinois State Plane System (ISPS)
9. Acknowledgment
References
Appendix A - Spatial Definition of the FMI Plane
Appendix B - Notes on Scale Compatibilities
Appendix C - Notes on Precision and Accuracy
Appendix D - Double Stereographic Projection
Appendix E - Lattice
Program Documentation and Source Codes
FERMILAB COORDINATE SYSTEMS
1. Introduction
Several years ago a DUSAF coordinate system was established
at Fermilab and the original documentation could not be traced.
It is a Cartesian coordinate system with no known map projection
associated with it. Therefore, it is not possible to directly
convert these DUSAF plane coordinates to the global geodetic (or
geographic) coordinate system using the appropriate Earth parameters.
The need for a map projection and a tie to a global coordinate
system also stems from the future global experiments being planned
at Fermilab. These global experiments use the Global Positioning
Systems (GPS) technology in which data is collected in the geodetic
coordinate system.
The objectives of this document are to relate Fermilab
to a global coordinate system, to define a mapping projection
and establish all the coordinate systems that will be used for
the Fermilab site and for the Fermilab Main Injector
(FMI) project, and to describe all the parameters
that are necessary for the several coordinate systems.
Since all lattice coordinates for all Fermilab and
FMI projects are provided in the DUSAF coordinate system, the
main objective is then to define a new assimilated DUSAF
coordinate system for the Fermilab site. This implies that the
new system will have the same origin and coordinate axes definitions
as the DUSAF coordinate system.
1.1 DUSAF Coordinate System
The DUSAF coordinate system is a right-handed
Cartesian coordinate system defined as follows:
The parameters that define the DUSAF coordinate system
origin are:
The DUSAF elevation Z is referenced to the DUSAF
(Vertical) Datum which is an arbitrary datum. At A0, Z = 720.000
ft implies that the elevation of A0 is 720 ft above the DUSAF
Datum.
1.2 Map Projection
The Survey Alignment and Geodesy group has adopted
a Double Stereographic Projection (see Appendix D) to define
a Fermilab Site Coordinate System (FSCS) for the Fermilab
site. The FSCS is referenced to the North American Datum
of 1983 (NAD83) and its reference ellipsoid of 1980 (GRS80).
The Double Stereographic Projection was chosen to map the GRS80
geodetic coordinates onto the conformal mapping plane which defines
the Fermilab Site Coordinate System. The Double Stereographic
Projection was also adopted to define a Local Tunnel
Coordinate System (LTCS) for the FMI project.
Before these new coordinate systems and other projection
systems are defined in greater details, the Geodetic Coordinate
System (GCS) will be described. The geodetic coordinate system
is the fundamental coordinate system with respect to which all
other coordinate systems are defined.
2. Geodetic Coordinate System (GCS)
GCS is a curvilinear coordinate
system, based upon a geocentric, bi-axial reference ellipsoid
(GRS80), called the North American Datum of 1983 (NAD83), with
axes coincident with those of the Geodetic Cartesian Coordinate
System, axis of rotation along the Z-axis (see section 3 below).
It is the fundamental coordinate system with respect to which
all other coordinate systems are defined. The geometric parameters
of the ellipsoid are:
where a is the semi-major axis of the
ellipsoid and f is the flattening of the ellipsoid.
The coordinates of a given point, Pi,
within this system are defined as:
i = Geodetic Latitude
i = Geodetic Longitude
Since the ellipsoidal height is directly related
to the orthometric height (elevation), this relationship will
be described in the following section.
2.1 Orthometric Height
The orthometric height, H, of a point, P, is defined
as the geometric distance between the geoid and the point, measured
along the plumb line through the point. The orthometric height
is based on the North American Vertical Datum of 1988 (NAVD88).
The orthometric height above the NAVD88 datum is determined by
where
The geoid height values are interpolated from a grid
of regularly-spaced estimates using the GEOID93 Model based on GRS80
(or WGS84, which is equivalent to NAD83, as defined below). The
actual computation is performed as an interpolation from a regularly-spaced
grid of points. The interpolation is accomplished by a locally fit biquadratic
function. The polynomial surface is fit to nine data points defining
the area surrounding the point where the interpolation is to take
place.
The NAVD88 orthometric heights are derived from heights
above the DUSAF datum using the expression:
where dHNAVD88 = - 0.17308 m is the correction
to tie the DUSAF datum to the NAVD88 datum.
The relationship between the ellipsoidal height in
the GCS system and the orthometric height above the DUSAF
datum is given by:
3. Geodetic Cartesian Coordinate System (GCCS)
GCCS is a geocentric,
right handed Cartesian coordinate system, with axes defined to
be coincident with those of the Reference Ellipsoid GRS80, used
for NAD83 datum. It is used as an intermediate system by
which other systems are converted to and from the
geodetic coordinate system GCS
. The orientation is defined as follows:
In these respects, NAD83 is similar to the other
modern global reference system, such as the World Geodetic System
of 1984 (WGS84). The Global Positioning Systems (GPS) data are
given in the WGS84 coordinate system. In principle, the three
dimensional coordinates of a single physical point should be the
same in both systems; in practice, small differences are sometimes
found. For these coordinate system definitions and transformations,
it can be assumed for all practical purposes that the NAD83 and
WGS84 are entirely coincident. There are standard formulas used
for conversion between the GCCS coordinates (XYZ) and the
geodetic coordinates (
) of the
GCS. Transformation between the GCCS coordinates (XYZ) and
other Cartesian coordinate systems are also possible.
4. Fermilab Site Coordinate System (FSCS)
The Fermilab
Site Coordinate System (FSCS) is an assimilated DUSAF
coordinate system. Its origin and rotation axes are located at
A0, preserving as nearly as possible the DUSAF coordinate system.
4.1 FSCS:XYZ
FSCS:XYZ coordinate system
corresponds to the lattice version of the FSCS. This coordinate
system was developed for the beamlines extracting from the Main
Ring and the Tevatron at A0. It is a right-handed
Cartesian coordinate system defined as follows:
The parameters that define the FSCS:XYZ coordinate
system origin at A0 are:
To relate the FSCS:XYZ system to the GCS
system, the ellipsoidal height of A0 is given as:
The Geodetic Azimuth defining the alignment of the
Y-axis at A0 is given as:
= 38o 16' 48.01429"
4.2 FSCS:XYH
FSCS:XYH is a
right-handed Cartesian coordinate system based
on a Double Stereographic Projection and heights above
the DUSAF datum. At the origin A0, the (XYH) coordinates in
this system are identical to the (XYZ) coordinates in the FSCS:XYZ
system. Figure 1 shows the relationship
between the FSCS:XYZ and FSCS:XYH systems.
FSCS:XYH is a two dimensional
mapping plane whose coordinates (X,Y) or (E, N; Easting, Northing)
are generated by a Double Stereographic Projection of geodetic
coordinates (
), with the origin defined as the point on the ellipsoid
corresponding to A0. The Double Stereographic Projection is performed
in two steps: namely, the projection from the reference ellipsoid
to a conformal sphere and from the sphere to a plane.
The basic parameters for performing the Double Stereographic
Projection are as follows:
0 = Geodetic Latitude of the origin
0 = Geodetic Longitude of the origin
= Geodetic Azimuth of the Y-axis (North) at the origin
The geodetic coordinates (),
are projected into E
and N using the double Stereographic projection, with the origin
defined as the point on the ellipsoid corresponding to A0. The
E and N coordinates are rotated about the Z-axis by the angle
(geodetic azimuth) to obtain the X and Y coordinates. The X
and Y coordinates are then re-scaled by the scale factor F0
to give true scale at the origin at 720 ft above the DUSAF datum.
False coordinates are applied at the origin.
The defined parameters of
the Double Stereographic Projection for the FSCS:XYH are
given below:
Geodetic coordinates at the origin A0
0 = N 41o 50' 14.312704"
0 = W 88o 15' 41.143123"
The relationship between the ellipsoidal height h0 in the GCS system and the orthometric height above the DUSAF datum is given by:
where H720DUSAF corresponds to 720 feet
above the DUSAF datum and dHNAVD88 = -0.17308 m is the
correction
to tie the DUSAF datum to the NAVD88 datum. N0 is
the geoid height (geoid93 model) at A0 and is equal to -32.78456
m. At any other point the ellipsoidal height is given as:
The orthometric height at A0 is given by:
The orthometric height at A0 in the FSCS =
219.45644 - 0.17308 = 219.28336 m. This relationship must be
considered when transforming between the FSCS and other
coordinate systems.
The orthometric heights are converted to heights
above the DUSAF datum using the expression:
Geodetic Azimuth of the Y-axis of FSCS at
the origin A0 is given by:
= 38o 16' 48.01429"
False coordinates applied at the origin are given
by:
At A0, the scale factor corresponding to the height
of 720 ft above the DUSAF datum (H720DUSAF) is given
by:
5. Local Tunnel Coordinate System (LTCS)
The Local
Tunnel Coordinate System (LTCS) was
established to meet the stringent accuracy requirements of the
FMI project. Its origin and rotation axes are located at a point,
CFMI, which lies at the centroid of the FMI Plane and whose (X,Y)
coordinates are in the FSCS. The coordinates in
the LTCS are defined in the FMI Plane. The FMI Plane is that
plane defined by the nominal designed orthometric heights of the
cell boundaries 308, 522, and 620. The coordinates of the cell
boundaries 308, 522, and 620 in the FMI Plane (and other coordinate
systems) are given in Table A1 in Appendix A. To convert the
LTCS coordinates to global geodetic coordinates the FMI Plane
must be tilted by a small angle to a projection plane
5.1 LTCS:XYZ
The LTCS:XYZ coordinate system corresponds
to the lattice version of the LTCS. The X-Y plane of the
LTCS is coincident with the FMI plane. It is a right-handed
Cartesian coordinate system defined as follows:
The parameters that define the LTCS:XYZ coordinate
system origin at CFMI are:
To relate the LTCS:XYZ system to the GCS
system, the ellipsoidal height of CFMI is given as:
The Geodetic Azimuth defining the alignment of the
Y-axis at CFMI is given as:
5.2 DSP:XYH
DSP:XYH is a right-handed
Cartesian coordinate system based on Double Stereographic Projection
and heights above the DUSAF datum. The (XYH) coordinates in this
system are identical to the (XYZ) coordinates in the
LTCS:XYZ system at the origin CFMI. The relationship
between the LTCS:XYZ
and DSP:XYH systems is shown in Figure 2.
DSP:XYH is a two dimensional
mapping projection plane whose coordinates (X,Y) or (E, N; Easting,
Northing) are generated by a Double Stereographic Projection of
geodetic coordinates (
The geodetic coordinates (
Geodetic coordinates at the origin at CFMI (Centroid
of the FMI Plane):
The ellipsoidal height in the GCS system,
h, is converted to an orthometric height above the DUSAF datum
using the same definitions and parameters as those given for the
FSCS:XYH coordinate height.
Geodetic Azimuth of the Y-axis of LTCS at
the origin CFMI is given by:
False coordinates applied at the origin are given
by:
5.3 LTCS:XYH
The actual working plane of reference for the FMI
tunnel is the FMI Plane. Therefore the coordinates in the DSP:XYH
projection plane must be related to the FMI Plane. The LTCS:XYH
coordinates in the Lattice Program (see Appendix E) refers to
the LTCS:XYH coordinates in the FMI Plane. The relationship
between the LTCS:XYZ, DSP:XYH
and FSCS:XYH
systems is shown in Figure 2.
To rotate the coordinates on the DSP:XYH projection
plane to the FMI Plane a seven-parameter transformation is performed
using the following expression:
where XLTCS:XYH is the vector
containing the (XYH) coordinates in the FMI Plane; XDSP:XYH
is the vector containing the (XYH) coordinates in the projection
plane; XTranslation is the vector containing
the translation parameters in XYH; R(
The transformation parameters from the DSP:XYH
projection plane to the LTCS:XYH FMI Plane are defined
as follows:
6. Local Geodetic System (LGS)
A left handed Cartesian coordinate system, defined
to be topocentric about a point, P, i.e., a coordinate system
with the origin at a point, P, of known geodetic coordinates.
The left-handed coordinate system is defined as follows:
It should be noted that there exists an infinite
number of local geodetic coordinate systems, dependent upon the
choice of point P.
7. Oblique Mercator Projection System (OMPS)
The Global Positioning Systems (GPS) data collected
at the Fermilab are in the geodetic coordinate system. Present
software available transform these data into a conformal mapping
plane using the Oblique Mercator Projection and the same basic
parameters as defined for the Double Stereographic Projection.
The Oblique Mercator Projection Coordinate System
(OMPS) is a two dimensional mapping plane whose coordinates
(X,Y) or (E, N), are generated by a Oblique Mercator Projection
of Geodetic Latitude and Longitude (
The defined parameters of the Oblique Mercator Projection
for the Fermilab site are given below:
The ellipsoidal height in the GCS system,
h, is converted to an orthometric height above the DUSAF datum
using the same definitions and parameters as those given for the
FSCS:XYH coordinate height.
Geodetic Azimuth of the Central Meridian (center
line) of the projection at the origin A0 is given by:
False coordinates applied at the origin are given
by:
At A0, the scale factor corresponding to the height
of 720 ft above the DUSAF datum (H720DUSAF) is given
by:
8. Illinois State Plane System (ISPS)
It might be necessary sometime to relate the FSCS
to an outside monument coordinates defined by the Illinois State
Plane Coordinate System (ISPS). The Illinois State Plane
Coordinate System is a two dimensional mapping plane whose coordinates
(x, y) or (E, N), are generated by a 1983 State Plane Transverse
Mercator Projection of Geodetic Latitude and Longitude
(
The parameters of the projection are given by:
False coordinates applied at the origin are given
by:
Central meridian scale factor at the grid origin
9. Acknowledgment
Thanks to all those who made this paper possible.
The geodetic committee comprising of the author, Virgil Bocean,
and George Wojcik defined and ratified the coordinate systems
and projection parameters. Virgil Bocean computed the projection
parameters which were also recomputed by the author for verification.
Virgil Bocean also wrote Appendix A. Terry Sager, Stu Lakanen,
John Greenwood, and the committee members reviewed this documentation.
Helpful discussions with all the above mentioned are also gratefully
acknowledged.
References
Leick, A., (1990). GPS Satellite Surveying, John
Wiley & Sons, Inc., New York.
Schwarz, C. R., (1989). North American Datum of
1983, NOAA Professional Paper NOS 2, Ed. Charles R. Schwarz, National
Geodetic Survey Rockville, MD.
Snyder, J. P., (1987). Map Projections - A Working
Manual. U.S. Geological Survey Professional Paper 1395. U.S.
Government Printing Office, Washington D.C.
Stem, J. E., (1989) . State Plane Coordinates System
of 1983. NOAA Manual NOS NGS. National Geodetic Information
Branch, NOAA, Rockville, MD.
The Fermilab Main Injector, Technical Design Handbook.
Fermilab Main Injector Department, Fermi National Accelerator
Laboratory, August 1994.
The FMI Collaboration Internal Communication. Fermi
National Accelerator Laboratory, December 12, 1995.
Thompson, D.B., Mepham, M.P. and R.R. Steves, (1977).
The Stereographic Double Projection. The Department of Surveying
and Engineering, University of New Brunswick, Fredericton, N.B.,
Canada. Technical Report No. 46.
Vanicek, P., and Krakiwsky, E. J., (1982). Geodesy:
The Concepts, North-Holland Publishing Company.
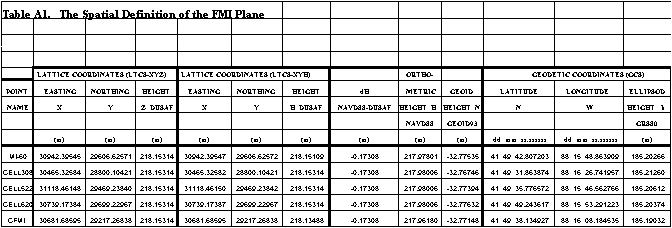
Appendix A
Spatial Definition of the FMI Plane
The objective of this section is to summarize the
definition of the plane that contains the Fermilab Main Injector
(FMI) with respect to the existing Tevatron and the local Earth
parameters. The details of the FMI location are determined by
the requirements for transfers of both protons and antiprotons
into the Tevatron.
The FMI is situated southwest of the Tevatron Ring.
The MI-60 straight section is parallel to the Tevatron F0 straight
section, and has the FSCS Azimuth = 301o 13' 53.9".
The two beamlines are separated by 11.823 m horizontally. The
design location of the MI-60 reference point is 13.222 m downstream
from the F0 TeV point, and offset from the TeV straight section
by 11.823 m (FMI Technical Design Handbook, 1994).
The FMI is designed to be a planar machine. The final
vertical definition of the FMI plane begins by specifying that
cell boundaries 522 and 620 are designed at the nominal orthometric
height of 218.15314 m (DUSAF Datum), and allow the initial constraint
on delta elevation between the FMI and TeV to vary (FMI Collaboration
Internal Communication, 1995). Based on the latest (1995) as found
elevation of the Tevatron F0 straight section quads string (220.48886
m DUSAF Datum), and the nominal FMI design elevation (218.15314
m DUSAF Datum), the FMI plane is located 2.33572 m below the Tevatron
beam.
Additionally, to account for the relative tilt of
the FMI and the Tevatron planes, and also for fully constraining
the FMI plane in the geodetic space with respect to the local
Earth parameters, it is further specified that the cell boundaries
522, 620, and 308 are placed at the same nominal design orthometric
height of 218.15314 m (DUSAF Datum). The coordinates of the cell
boundaries 308, 522, and 620 in the FMI Plane (and other coordinate
systems) are given in Table A1.
Appendix B
Notes on Scale Compatibilities
Sc Distance between
two points inverted from the coordinates.
Sa Actual distance between
two points as measured in reality.
GCCS This is
a Cartesian coordinate system, which does not involve the use
of a projection. Sc and Sa
will be equal.
FSCS:XYZ This is a
Cartesian coordinate system. Sc and Sa
will be equal.
FSCS:XYH This is a projection
coordinate system that has been re-scaled by the appropriate scale
factor F to be compatible with the 720 ft above DUSAF datum.
Therefore a two dimensional distance Sa measured at
the 720 ft height is related to Sc by the expression:
where the projection scale factor k is equal to 1
at the origin.
Away from the 720 ft above DUSAF datum an additional
scaling is required:
where Fh is the height scale factor at
the measurement height, and F720 is the standard height
scale factor (= 1.000029251309483).
LTCS:XYZ This is a
Cartesian coordinate system. Sc and Sa
will be equal.
LTCS:XYH This is a
projection coordinate system that has been
re-scaled by the appropriate scale factor F to be
compatible with the 715.664 ft above DUSAF datum. In a similar
definition to that used for
the FSCS:XYH, the relationship between the
two dimensional distance Sc and Sa is:
where k is the projection scale factor, equal to
1 at the origin CFMI.
Fh is the height scale factor at the measurement
height, and FCFMI is the standard height scale factor
(= 1.000029046120306).
LGS
This is a Cartesian coordinate system. Sc and
Sa will
be equal.
OMPS This is a projection
coordinate system that has been re-scaled by the appropriate scale
factor F0 (= 1.000029251309483) to be compatible with
the 720 ft above DUSAF datum.
In a similar definition to that used for the FSCS:XYH,
the relationship between the two dimensional distance Sc
and Sa is:
where k is the projection scale factor, equal to
1 along the center line of the projection (azimuth ); Fh
is the height scale factor at the measurement height; and
F720 is the standard height scale factor at the DUSAF
datum.
ISPS This is a projection
coordinate system that has not been re-scaled by to any datum.
The relationship between the two dimensional distance
Sc and Sa is:
where k is the projection scale factor, equal to
0.999975 along the central meridian line of the projection (azimuth
); Fh is the height scale factor at the measurement
height, equal to 1 on the ellipsoid.
Appendix C
Notes on Precision and Accuracy
The precision of the conversion from one coordinate
system to another has been specified by the SAG group to be 1x10-7
m. Therefore in converting from one system to another and
back again, the coordinates will be compatible to this level.
In terms of accuracy, it should be noted that a coordinate
conversion cannot compensate for the inaccuracies in the original
data. Therefore in converting to the ISPS, for example,
the compatibility with other data can only be as good as the survey
that defined the geodetic coordinates of the point A0.
Appendix D
Double Stereographic Projection
Traditional geodetic computations are carried out
on the surface of a biaxial ellipsoid (ellipsoid of revolution),
which is the mathematical figure that is the most convenient representation
of the size and shape of the earth. To perform the same computations
on a plane, it is necessary to map the ellipsoidal information
(points, angles, lines, etc.) on a plane mapping surface. A convenient
mapping for geodetic purposes is a conformal mapping in which
ellipsoidal angles are preserved on the mapping plane.
The Stereographic projection of an ellipsoid of revolution
can be approached by a double projection (hence double Stereographic
projection), in which the biaxial ellipsoid is conformally mapped
to a sphere, which is then "stereographically" projected
to a plane.
The Stereographic projection of a sphere to a plane
has the following properties (Thompson, et. al., 1977):
(i) It is a perspective projection, the features
being projected from the sphere onto the plane from a common point
of perspective. This perspective center lays on the sphere, and is the
antipodal point of the point at which the plane is tangent to the sphere.
(ii) It is an azimuthal projection, characterized
by the fact that the direction, or azimuth, from the center of the
projection to every other point on the map is shown correctly.
(iii) It is a conformal projection, the relative
local angles about every point on the map are shown correctly (angles not
distorted).
(iv) Scale increases away radially from the origin
(center) of the projection.
(v) Great circles are projected as circles.
The Stereographic projection of a sphere to a plane
is the only true perspective projection of any kind that is also
conformal. There is no mapping of an ellipsoid to a plane that possesses
all the characteristics of the Stereographic mapping of a sphere
to a plane. For the conformal mapping of the biaxial ellipsoid
on a plane, the ellipsoidal data is first mapped conformally on
to a sphere. Then, a second conformal mapping of the spherical
data to the plane completes the double Stereographic projection.
The result is a conformal mapping of ellipsoidal data on a plane,
since the two mappings are conformal.
The Stereographic projection is the most widely used
azimuthal projection, mainly used for portraying large areas of
similar extent in all directions. The Stereographic projection
is very suitable when areas of interest are circularly shaped,
like the FMI area. Since all the surveying activities will occur
along the path of the ring, choosing the origin of the projection
at the centroid of the FMI Plane has as a result that the scale
along the tunnel will be standardized to the same scale factor.
The differences created by the fact that the FMI shape is not
perfectly circular is very insignificant.
Appendix E
Lattice Program Documentation and Source Codes
= 38o 16' 29.97831"
), with the origin defined as the point
on the ellipsoid corresponding to CFMI. This projection plane
is tilted from the LTCS:XYH FMI plane by an angle 
,
see Figure 2. The basic parameters of the projection are the same as those
of FSCS:XYH. The parameters for FMI have been selected
to minimize the effect of the point scale factor for all points
around the FMI tunnel. The parameters of the projection are given
below.
)are projected into E
and N using the double Stereographic projection, with the origin
defined as the point on the ellipsoid corresponding to CFMI.
The E and N coordinates are rotated about the Z-axis by the angle
(geodetic azimuth) to obtain the X and Y coordinates. The X
and Y coordinates are then re-scaled by the scale factor F0
to give true scale at the origin at 715.664 ft above DUSAF datum.
False coordinates are applied at the origin.
The defined parameters of the Double Stereographic
Projection for the DSP:XYH are given below:
0 = N 41o 49' 38.134927"
0 = W 88o 16' 08.184535"
= 38o 16' 29.97831"
At CFMI , the scale factor corresponding to the height
of CFMI above the DUSAF datum (HCFMIDUSAF) is given
by:
X,Y,H)
* XDSP:XYHX,Y,H)
is the rotation matrix; and S is the scale.
X
= 2.07594 arcsec
Y
= -0.74326 arcsec
H
= 0.00000 arcsec Fixed
), in the GCS system.
0 = N 41o 50' 14.312704"
0 = W 88o 15' 41.143123"
= 38o 16' 48.01429"
) in
the GCS system. The zone used in the vicinity of Fermilab
site is the Illinois East Zone #1201 as given by the National
Geodetic Survey (Stem, 1989).
0 = N 36o 40' 00.00000"
0 = W 88o 20' 00.00000"
.
Sa
.Sa
.Sa
.Sa
On page 3,
Geodetice Cartesian Coordinate System
should read
Geodetic Cartesian Coordinate System
On page 6,
XGC XGC
XGC = YGC should read XGC = YGC
YGC ZGC
XLG XLG
XLG = YLG should read XLG = YLG
YLG ZLG
On page 8,
XFXYZ XFXYZ
XFXYZ = YFXYZ should read XFXYZ = YFXYZ
YFXYZ ZFXYZ
XLG XLG
XLG = YLG should read XLG = YLG
YLG ZLG
On page 8,
a = Geodetic Azimuth of the Fermilab (XYZ) Origin
should read
= Geodetic Azimuth
of the Fermilab (XYZ) Origin
On page 12,
= Geodetic Azimuth
of the Fermilab (XYZ) Origin